Bernhard Peter
Fallstricke beim Zeichnen von Helmdecken

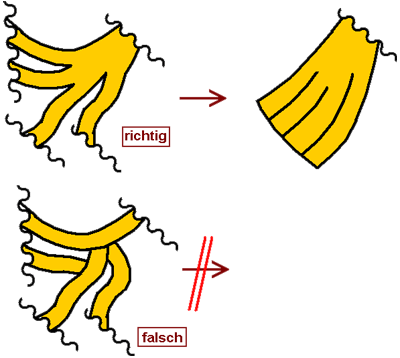
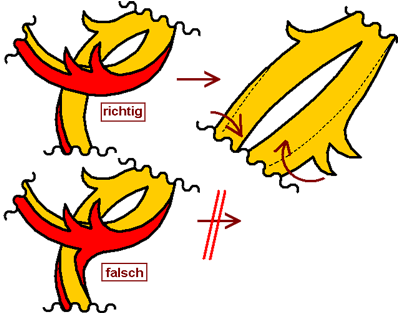
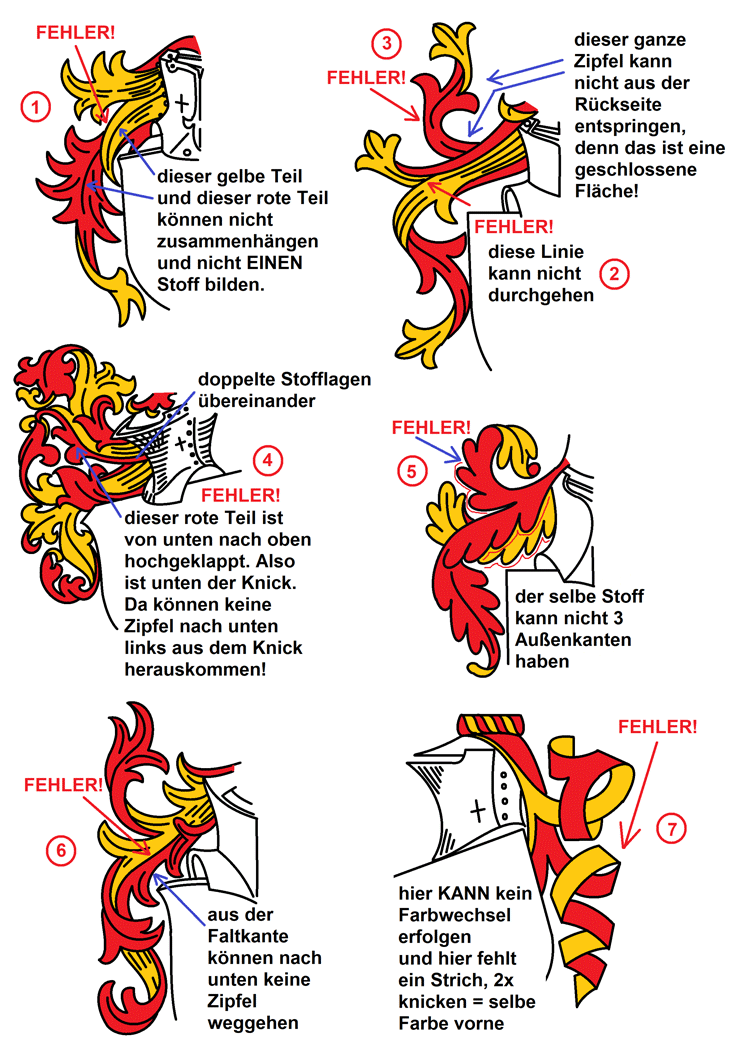
1. Fallstrick: Eine Helmdecke basiert auf einem Tuch
Weil das Zeichnen von Helmdecken vielen Menschen immer noch Schwierigkeiten macht, hier ein paar Anmerkungen zu häufigen Fehlern. Eine Helmdecke ist ihrem Wesen nach ein Tuch. Ein Tuch, das auf den Helm gelegt wird und zu beiden Seiten herabfällt. Wie die Seiten gestaltet werden, in wie viele Zaddeln das Tuch aufgelöst wird, wie die ganzen Zipfel im Raum stehen, das unterliegt der künstlerischen Freiheit. Nicht der künstlerischen Freiheit unterliegt die schlichte Tatsache, daß es sich um ein Tuch handelt. Weder um Blumengirlanden, noch um Laubgewinde und auch nicht um spiralige Linien ohne Körperlichkeit. Das Wort "Tuch" beinhaltet auch die schlichte Tatsache, daß es sich um ein Stück Stoff handelt. Dieser wurde zwar mit der Schere bearbeitet, eingeschnitten, zugeschnitten, ausgeschnitten, aber es bleibt ein Tuch mit Vorder- und Rückseite, das man wieder vom Helm abnehmen und auf einer ebenen Fläche ausbreiten kann. Eine Helmdecke ist nicht aus mehreren Streifen zusammengenäht, an den Zaddeln wird auch nicht gestückelt wie bei einer künstlichen Haarverlängerung. In der plakativen Darstellung unten wird deutlich, daß eine auch noch so komplexe Auflösung in Zaddeln immer noch auf der schlichten Tuchform beruht, die eben eingeschnitten wird. Angenähte Teile sowie Stücke, die grundlos irgendwohinter hervorkommen und sich nicht logisch aus der Tuchfläche ergeben, sind nicht korrekt.

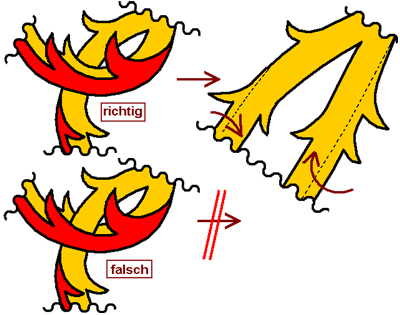
2. Fallstrick: Eine Helmdecke ist ein zusammenhängendes Tuch
Man muß es leider auch erwähnen: Eine Helmdecke ist ein zusammenhängendes Tuch. Genauso wenig, wie Teile der Helmzier lose an Lufthaken aufgehängt sein können, sondern Anbindung an Materie benötigen, so kann es bei einer Helmdecke keine losen Teile geben, die im Zustand der Schwerelosigkeit neben der restlichen Materie existieren. Der Blick in die Wappenrollen-Eintragungen der letzten Jahre zeigt, daß das durchaus erwähnt werden muß.

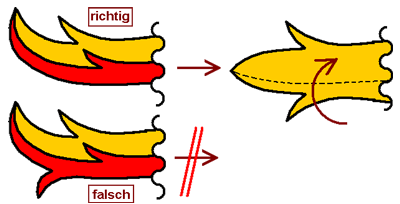
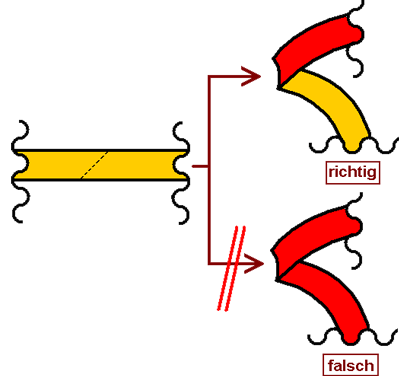
3. Fallstrick: Eine Helmdecke kann keine drei gleichgerichteten Außenränder haben
Die Hauptforderung an eine korrekte Helmdecke ist, daß sie technisch realisierbar ist. Um das zu sehen, braucht man ein bißchen räumliches Vorstellungsvermögen. Ein Stück Stoff hat eine Vorderseite und eine Rückseite, keine dritte Seite. Fakt ist, daß ein normaler Fetzen Stoff - quer betrachtet - zwei Ränder hat. Man kann eine dritte Kante kriegen, wenn man den Stoff faltet oder entsprechend weit biegt. Dann muß die Randgestaltung aber auch dazu passen, denn an der Falte (gestrichelte Linie) dürfen auf der ganzen Länge keine Zaddeln sein, nur an den Außenkanten. Das obere Beispiel ist richtig, die ganze untere Kante ist der Falz, wenn man das rote Stück herunterklappt, hat man wieder ein ebenes Stück Stoff. Würde man das im unteren Fall tun, wird klar, daß der untere rote, hakenförmige Zipfel nicht sein kann. Eine solche Gestaltung ist technisch nicht möglich und daher falsch.

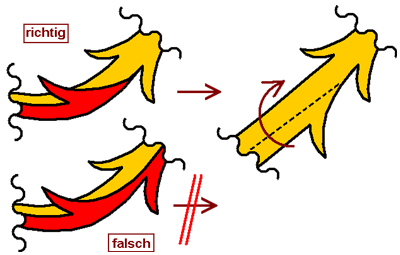
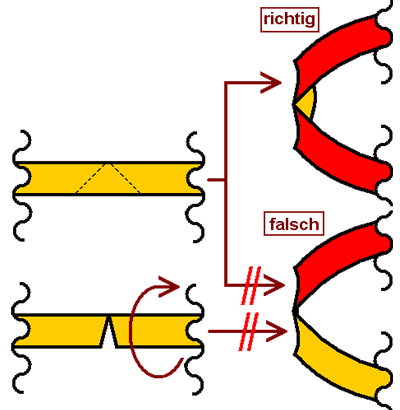
Genau das Gleiche gilt für folgendes Beispiel: Ausgehend von der rechten Skizze, die das ausgebreitete und zugeschnittene Stück Tuch zeigt, wird die untere rechte Seite hochgeklappt. Weil der Falz aus einer geknickten Fläche entstand, dürfen an ihm auf seiner ganzen Länge keine Zaddeln sein. Der untere Fall ist fehlerhaft - würde man hier den roten Teil herunterklappen, würde der Stoff mindestens an der Engstelle reißen - was klar macht, daß so etwas zwar auf dem Papier geht, niemals aber technisch realisierbar ist. Damit ist es ebenfalls falsch. Eine an einer beliebigen Stelle senkrecht zur Ausbreitungsebene geschnittene Helmdecke ergibt immer, das liegt in der Natur des Stoffes, eine unverzweigte Profillinie.

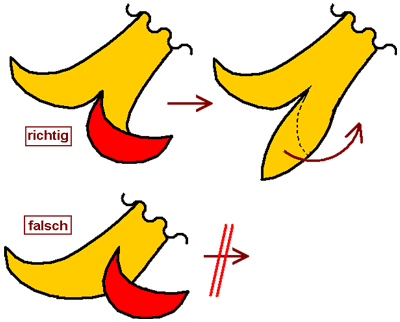
4. Fallstrick: Ein Stück Stoff kann nicht mitten aus der Fläche entspringen
Und mitten aus der Stoff-Fläche kann nicht einfach ein weiterer Lappen entspringen. Im oberen Fall entsteht der rote Zipfel durch Umschlagen des einen der beiden fischschwanzartigen Zipfel nach innen, dadurch wird die Außenseite sichtbar. Im unteren Fall steht der Zipfel mitten auf der geschlossenen Fläche - technisch unmöglich und daher falsch. Betrachten wir es genauer: Der gelbe Teil ist Innenseite, nicht sichtbar ist die rote Rückseite, denn keine Partie ist umgebogen. Mittendrin nun der rote Haken - offenbar Außenseite. Ein Stück Stoff hat eine Vorder- und eine Rückseite. Das sind genau zwei Seiten und nicht drei und auch nicht vier. Die untere Gestaltung ist daher falsch.

Bei der Aufgabelung eines Stoffstreifens in zwei Teilstreifen sollte darauf geachtet werden, daß der Schnitt eine Teilungslinie ist, die für beide Teilstreifen gilt. Im linken Beispiel ist das eine saubere Sache: Schnitt, und ab der Trennung hat jeder Streifen sein Eigenleben. Doch wie wurde im mittleren Fall geschnitten? Damit eine solche Sache möglich würde, müßte man mit einer Rasierklinge horizontal in ein vor einem liegendes Stück Stoff einschneiden, den Stoff in zwei übereinanderliegende einzelne Lagen spalten, das Tuch praktisch in seiner eigenen Ebene in einen "Oberstoff" und einen "Unterstoff" aufschneiden - oder nähen. Also ist eine solche Aufspaltung, wo aus einer Lage Stoff an der Überlappungsstelle wie durch Zauberhand zwei Lagen Stoff mit zwei Vorderseiten und zwei Rückseiten werden, nicht tatsächlich realisierbar und damit falsch. Ganz anders wieder im rechten Fall: Hier ist das Tuch in Verlängerung der Schnittlinie in einer Art "Bergfalte" (Begriff aus dem Origami) gefalzt, beide Teilstreifen rollen sich ein, der vordere nach vorne, der hintere nach hinten - das geht sehr wohl, aber dann sind die Farben auch anders verteilt.

5. Fallstrick: Überblick behalten!
Je komplexer und üppiger die Decken gestaltet werden, desto unübersichtlicher werden sie. Und wo es unüberschaubar wird, schleichen sich schnell Fehler ein. Im folgenden Beispiel besteht der gezeigte Abschnitt aus zwei Hauptstreifen, von denen der untere vor dem oberen rübergezogen wird, U-förmig in sich eingeschlagen. Hier ist auf saubere Trennung zu achten. Oben geht der gesamte Streifen vor dem anderen her, ohne Verbindung zu diesem. In der unteren Abbildung läuft die Außenseite des vorne liegenden Streifens über in die Außenseite des hinteren Streifens. Rein technisch wäre das machbar, wenn der Stoff nicht ganz eingeschnitten wäre, sondern abschnittsweise geschlitzt. Falsch wird es aber dadurch, daß die Hinterkante des vorderen Streifens sichtbar bleibt - denn damit wird dieses Konstrukt technisch unmöglich, der Stoff hätte eine Seitenkante zuviel. Die untere Abbildung, so gefällig sie aussieht, ist nicht realisierbar und damit falsch.

6. Fallstrick: nicht durchwachsen lassen!
Eine weitere Falle lauert in der Staffelung im Raum. Je komplizierter die Verschlingungen, desto leichter schleichen sich Fehler diesen Typs ein. Man beachte stets, daß ein Stoffabschnitt als Ganzes vor oder hinter einem anderen Stoffabschnitt hergeht. Oben geht der vordere Streifen komplett vor dem hinteren vorbei. Unten dagegen geht die vordere Kante vor dem hinteren Streifen vorbei, die hintere Kante des vorderen Streifens aber hinter dem hinteren Streifen - was technisch nur möglich wäre, wenn man in den vorderen Streifen in der Mitte einen Schlitz schneidet und den hinteren Streifen dort hindurchfädelt - das ist aber nicht das Wesen eines im Wind flatternden Tuches. Das Zeichnen einer Helmdecke soll nicht zu Stoff-Origami ausarten. Daher ist die untere Darstellung falsch.

Bezüglich der Farbe ist stets darauf zu achten, daß ein Stück Stoff immer in der gleichen Farbe aus einem verdeckten Zustand hervorkommt wie es hinter einer anderen Bahn verschwunden ist, außer wenn in der Verdeckung ein Turn (eine Drehung) passiert. Das hört sich trivial an, ist aber in der Praxis ein häufiges Problem. Zur besseren Übersichtlichkeit läßt man besser keine Turns hinter etwas passieren, denn das Ergebnis verwirrt den Betrachter.

7. Fallstrick: Jeder einzelne Knick ergibt einen Farbwechsel
Ein weiterer Fallstrick lauert bei den Farbwechseln selbst. Dabei ist es so einfach: Einmal knicken: Farbe wechselt. Zweimal knicken: Farbe bleibt. Deshalb ist die obere Abbildung richtig: Vor dem Knick ist Außenseite (rot) sichtbar, nach dem Knick ist Innenseite (gold) sichtbar. Helmdecken, die vor und nach einem Knick die gleiche Farbe zeigen, sind falsch.

Und wenn zweimal geknickt wird, bleibt die Farbe bzw. ist wieder die selbe. Z. B. diese Art der Knickung ist nur möglich mit zwei Falzlinien, die in ca. rechtem Winkel aufeinander stehen. Auch wenn die beiden roten Flächen dominieren, darf nicht vergessen werden, daß der Stoff zwischen beiden Knickstellen seine Körperlichkeit nicht einfach verliert. Im oberen Fall ist es so gezeichnet, daß man ein bißchen goldene Innenseite des dazwischenliegenden Stoffes sieht. Im unteren Fall ist es dagegen so gezeichnet, daß man genau auf die Kante guckt und das dreieckige Zwischenstück dadurch nicht sichtbar in Erscheinung tritt. Es ist aber da und nicht verschwunden, es steht nur senkrecht zum Betrachter, und deshalb müssen auch hier beide sichtbare Teilstücke die gleiche Farbe haben. Man könnte nun argumentieren, der Streifen sei an dieser Stelle eingeschnitten. Auch das bessert die Situation nicht, denn wenn wir die Stellen rechts und links des Schnittes einfach auseinanderbiegen, haben sie immer noch die gleiche Farbe. Und wenn wir an der Engstelle eine Hälfte um 180 Grad verdrillen, so können zwar die Streifen unterschiedliche Farben haben, aber die Schnittkanten können nicht zur gleichen Seite der Engstelle sein - dann wäre eine nach vorne und die andere nach hinten zu zeichnen. Wie man es auch dreht und wendet, die untere rechte Abb. ist in jedem Falle falsch.

Weiterhin sollte man darauf achten, daß an einer Knickstelle die Außenkante des Knicks einen realistischen Winkel hat, d. h. senkrecht zur Winkelhalbierenden beider Teilbänder steht. Es ist nicht plausibel und auch nicht schön, wenn es da zu größeren Abweichungen kommt. Technisch möglich wäre das nur, wenn die ungeknickte, auf dem Tisch ausgebreitete Partie von vornherein abgewinkelt zugeschnitten wäre.

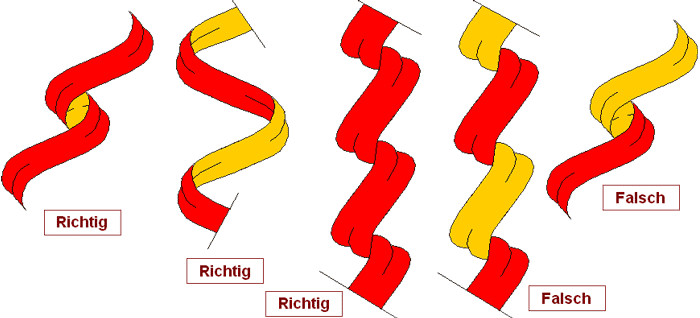
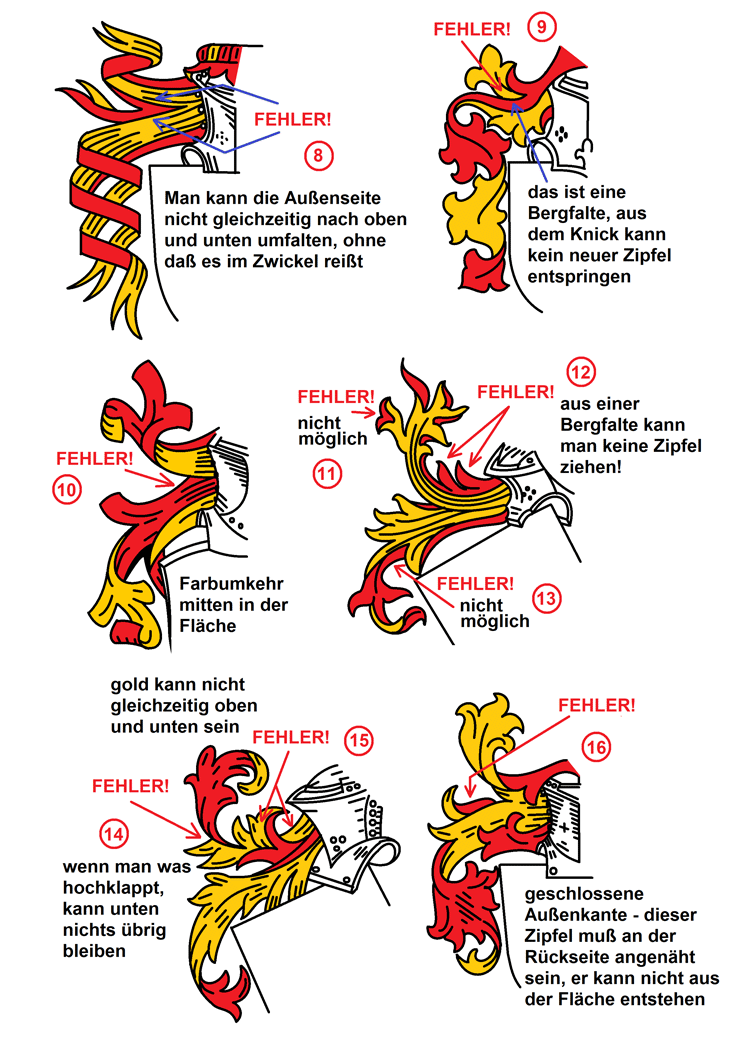
8. Fallstrick: 180°-Drehung - Farbe wechselt, 360°-Drehung - Farbe bleibt
Ganz analog gilt im folgenden Beispiel: Wenn sich Streifen einer Helmdecke spiralartig rollen, wechselt die Farbe bei einer 180-Grad-Drehung und bleibt die Farbe bei einer 360-Grad-Drehung. Eine spiralig gelegte Decke hat außen immer die selbe Farbe. Wenn man Farbwechsel beabsichtigt, sollte daher immer ein Zwischenstück sichtbar bleiben. Solange eine Helmdecke ein Tuch ist - was nun einmal definitionsmäßig Voraussetzung ist, ist eine Darstellung wie die zweite von rechts im Bild falsch.

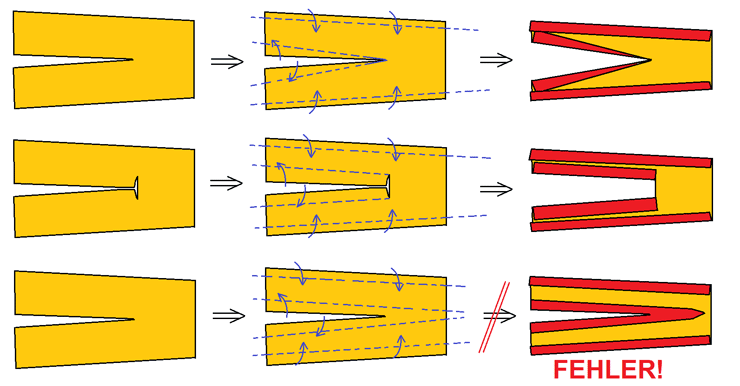
9. Fallstrick: Eine Helmdecke ist ein Tuch, kein Gummituch
Bei Helmdecken sind Einschneiden und Umknicken ein legitimes und sogar notwendiges Gestaltungsmittel. Man sollte daran denken, daß man an einer an beiden Seiten offenen Kante auf die ganze Länge in einheitlicher Breite einfalten kann, bei einer nur an einer Seite offenen Kante aber maximal bis zum Einschnittende, und mit abnehmender Breite, denn wenn der Einschnitt zu Ende ist, ist auch der Stoff zu Ende (erste Reihe). Gleichbleibende Breite kann man nur mit zusätzlichen Schnitten senkrecht zum ersten langen Schnitt erreichen (zweite Reihe). Und man sollte immer beherzigen: Wenn man Stoff eingeschlagen hat, ist er danach dort, wo er vorher war, weg! Deshalb sieht die Variante der zweiten Reihe unschön aus. Das Auslaufenlassen wie in der ersten Reihe sieht im Kontext schöner aus. Was überhaupt nicht geht, ist, den Stoff nach oben und nach unten weg vom Schlitz zu falten und dann zu zaubern, indem man ihn seitlich vom Schlitz weitergehen läßt (dritte Reihe). Ein Stoff läßt sich aber nicht wie Gummifolie ziehen - sowas geht nicht! Ebensowenig geht es, eine gezaddelte Helmdecke reihum, jedem Zipfel folgend, mit einem gleichdicken Bord in Außenfarbe zu versehen, das funktioniert nicht, weil es bei jeder Außenspitze eine zweifach übereinandergelegte Faltung erzwänge und in jeder Kerbe zu einem Materialriß führen würde. Wer es nicht glaubt, probiere es bitte mit echtem Stoff aus.

10. Fallstrick: Helmdeckenfehler für Fortgeschrittene - in Tiefenprofilen denken!
Auf den ersten Blick ist das eine wunderschöne Decke. Sie basiert auf einem hier ungenannten Wappenrolleneintrag der letzten Jahre und ist von allen sonstigen Fehlern bis auf einen bereinigt und entsprechend verändert worden. Dieser verbleibende Fehler ist schwer zu finden und erfordert ein gewisses Maß an Eindenken in die dreidimensionale Anatomie einer Helmdecke. Also, wo ist der Fehler?

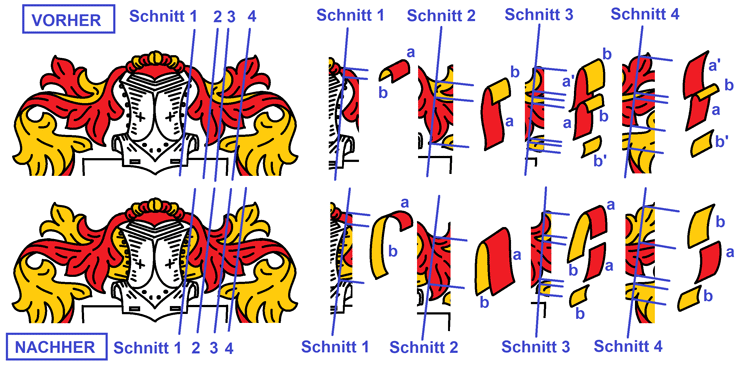
Dieses Beispiel soll zeigen, wie man Helmdecken analysiert, oder andersherum gedacht, aufbaut. Zum Verständnis, was hier vorliegt, stellen wir uns vor, die Helmdecke an den mit "Schnitt 1", "Schnitt 2" etc. markierten Stellen vertikal senkrecht zur Ausbreitungsrichtung der Decke zu zerschneiden. Wir erhalten dann ein Tiefenprofil der Decke. Es muß, das wurde bereits oben erläutert, eine unverzweigte Linie entstehen, die in ihren Auf- und Abschwíngungen ein für die Stelle charakteristisches Tiefenprofil aufbaut. In der Graphik sind 5 Schnittstellen markiert, rechts oben sind in leichter perspektivischer Verbreiterung die erhaltenen Profile dargestellt; die Verbreiterung erfolgte, damit man die Farben darstellen kann. Wir erkennen, daß die Decke insgesamt aus maximal fünf Ebenen besteht, die a, b, c, d und e benannt werden. Die tiefste Ebene, e, ist rechts und links des Helmes, es ist die goldene Fläche ganz hinten, wo es nicht mehr weitergeht. Die oberste Ebene, a, ist das, was am Helm oben und an den Schläfen nach oben umgeklappt wird. Deshalb gibt es Ebene a nur heraldisch links bei den Schnitten 4 und 5, nicht aber bei den Schnitten 1, 2 und 3 heraldisch rechts. Wenn man bei Schnitt 3 den von oben herabhängenden roten Zipfel nochmal nach oben umklappen würde, dann hätte man auch hier eine Ebene a. Ist aber nicht so, deshalb beginnen wir dort mit rot = b. Von Bedeutung ist, daß die Helmdecke in ihrem oberen Teil noch eine Zwischenwelle hat, die mal sichtbar ist wie in Schnitt 2 und 5, mal unsichtbar ist wie in Schnitt 3. Diese Zwischenwelle besteht aus den Ebenen c und d. Bitte vergleichen Sie in Ruhe die mit "Aufbau" gekennzeichneten Tiefenprofile rechts mit der gezeichneten Decke links, so lange, bis die Zeichnung links dreidimensional vor Ihrem inneren Auge existiert.

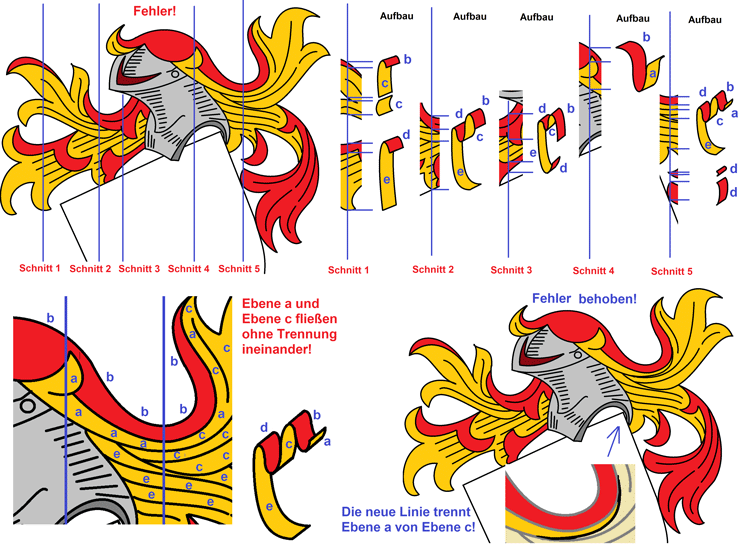
Und wenn man die Decke so analysiert hat, findet man auch das Problem: In Schnitt 5 haben wir drei goldene Flächen unterschiedlicher Tiefe, a, c und e. In Schnitt 4 wird offensichtlich, daß das Tuch vom Helmdach, das noch einmal aufgeworfen wird, um seine hochgeklappte Innenseite als Schicht a zu zeigen, die alleroberste Schicht ist. Lassen wir von da aus den Blick nach optisch rechts wandern: Diese Fläche geht nahtlos in die goldene Ebene c über. Ebene a verschmilzt in der Zeichnung mit Ebene c. Hier wird also eine goldene Fläche oberhalb der roten Fläche (a) mit einer goldenen Fläche unterhalb der roten Fläche (c) verschmolzen. Das ist so wie bei den Graphiken von M. C. Escher: Man erzeugt graphisch einen zeichnerisch täuschenden Kontext, der real nie möglich wäre. Das Problem ist zeichnerisch durch eine einzige Linie zu lösen: Man muß Ebene a durch eine neue Linie beenden und sauber von Ebene c trennen. Unten rechts in der Schildfläche zeigt die Einsatzgraphik, wie einfach man das mit der neu eingezogenen, tiefschwarzen Linie retten kann. Jetzt ist klar: oberhalb dieser neuen Linie ist die hochgeklappte oberste Lage oberhalb der roten Ebene, rechts und unterhalb der Linie ist die Ebene der Zwischenwelle unterhalb der roten Ebene.

Wie dieses Denken in Lagen und Schnitten bei der Aufspürung von Fehlern helfen kann, zeigt auch folgendes Beispiel, ebenfalls auf einem realen Fall beruhend. Diese Decke (links) hat zwei Schwachstellen, mit den roten Kreisen markiert. Seitlich des Helmes zieht sich ein breiter Streifen nach außen, der oben und unten nach vorne eingeschlagen ist - alles korrekt. Doch dahinter kommt oben ein dünnerer Streifen hervor, der sich zum oberen Drittel der Decke entwickelt. Dieser Streifen kann nicht einfach aus der Rückseite eines geschlossenen Stoffstreifens entspringen, er müßte separat geschneidert und hinten angenäht werden - kein wünschenswertes Helmdeckenkonzept. Er kann auch nicht einfach aus der Bergfalte = umgeknickter Stoff gezaubert werden. Im Schnitt 1 wird das deutlich: Die goldene Innenseite c wird von zwei nach vorne umgeschlagenen Rückseiten b gesäumt, oben und unten. Die formbaren Außenkanten liegen mehr oder weniger parallel nach innen und vorne eingeschlagen. Um die dahinter liegende Ebene c' zu ermöglichen, ist keine logische Biegung des Stoffes machbar, und es besteht keinerlei Anbindung zu einer formbaren Außenkante. Ebene c' entspringt einfach so auf der Rückseite von c, was technisch ohne Annähen oder Ankleben nicht möglich ist. Im Schnitt 1 sehen wir das Problem im Aufbau: Die Linie ist verzweigt, was nun mal bei einer Lage Stoff nicht geht. Wie ändern wir das? Wir lassen den ganzen oberen Teil logisch richtig dadurch entstehen, daß Ebene b noch ein zweites Mal umgebogen wird, diesmal nach oben, so daß als oberste Lage Ebene a entsteht. Das wird in der Mitte gezeigt: Der ganze obere Teil der Decke wird aus dem umgeschlagenen Rand b durch erneutes Hochfalten gezogen. Im Schnitt 1 sehen wir den Aufbau 1 als geschlossene, stetige und unverzweigte Linie. So ist es technisch möglich.

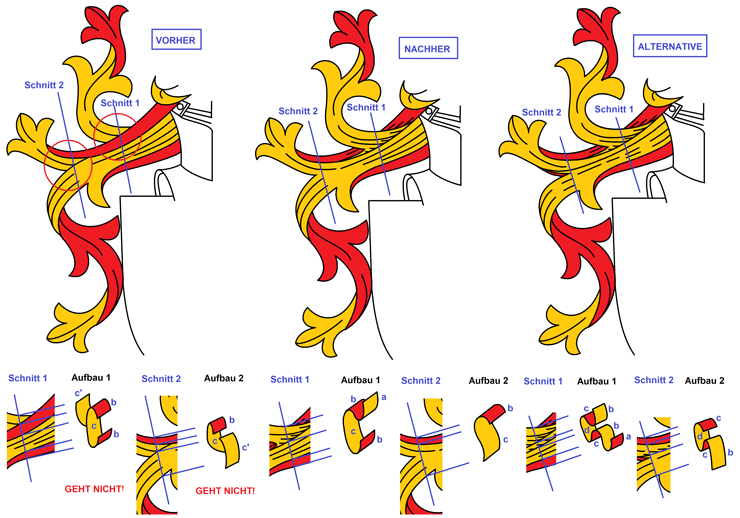
Das zweite Problem ist in Schnitt 2 markiert. Oben sehen wir eine rote, in einer Bergfalte nach unten umgeschlagene Außenseite, Ebene b. Darunter sehen wir aber nicht eine goldene Innenseite, sondern zwei alternative goldene Innenseiten, die durch eine durchgezogene Linie voneinander getrennt sind, und die durchgezogene Linie nimmt Kurs auf die Bergfalte, als wolle sie hinter dem roten "Vorhang" mit dem oberen Knick verschmelzen. Die zweite Ebene gibt es also doppelt, c und c'. Auch hier zeigt der Aufbau, daß durch die Strichführung eine verzweigte Schnittlinie entsteht, technisch nicht möglich. Das ist einfach zu lösen (Mitte), indem wir Ebene c und Ebene c' verschmelzen, also die durchgezogene Linie entfernen.

Hier stellt sich die Frage, ob es nicht auch anders ginge, ob man irgendwie die dahinter liegende Ebene erhalten könnte. Das führt zu einer zweiten Lösung (rechts): Dazu führen wir eine zweite Welle ein, indem wir die Ebene des Tuches in der Fläche greifen und nach oben raffen. Die tiefste Ebene ist jetzt der Hintergrund d, der oben nach vorne zu c umgeschlagen wird. Unten bilden c und b die hochplissierte Welle im Tuch. Das wäre eine zweite denkbare Lösung, die in der Tat eine durchgezogene Linie rechtfertigte. Dann darf diese durchgezogene Linie aber nicht Kurs auf die obere Umschlagkante der Helmdecke nehmen, sondern sollte als Welle sichtbar sein, wie in der rechten Abb. Auch sollte man im Zwickel irgendwie zeichnerisch deutlich machen, daß das Tuch hinter der Welle wieder ein Stück nach unten geht, wie z. B. durch ein winziges Stückchen roter Rückseite in der Einkerbung. Ob das überzeugend zeichnerisch dargestellt werden kann, ist eine andere Frage: Technisch wäre dieser zweite Weg machbar, zeichnerisch besser sieht der erste Weg (Mitte) aus, denn eine schöne Helmdecke zeichnet sich durch schnelle Erfaßbarkeit und hohe Plausibilität der Konstruktion aus.

Im nächsten Beispiel sehen wir oben links in der Graphik den oberen Teil einer total vermurksten Helmdecke, auch dies nach einem realen, hier nicht genannten Fall gezeichnet. Als erstes fällt auf, daß rechts und links des Helmes gar nichts ist: Gähnende Leere. Die Helmdecke scheint nur ein bißchen das vordere Helmdach zu bedecken und ansonsten das Hinterhaupt und den ganzen Nacken frei zu lassen. Das ist schlechter Stil, weil genau hier die Helmdecke vor Sonne schützen soll, aber das ist leicht korrigiert, indem man die Innenseite b hinter dem Helm bis unten zieht, die korrigierte Zeichnung ist links unten zu sehen. Der Vergleich der beiden Schnitte 1 zeigt die simple Verlängerung von b. Schwieriger wird es, zu verstehen, was genau rechts und links seitlich des Helmes passiert ist. Die Außenfarbe a ist offensichtlich Rot, zu sehen am vorderen Helmdach. Von hinten ist daneben die goldene Innenseite b oben nach vorne umgeschlagen (Schnitt 2), als ob sie Außenseite wäre. Im Grunde findet hier ein Funktionswechsel statt: In Schnitt 1 war Rot a die Außenfarbe, in Schnitt 2 ist es Gold b. Das Gold b ist hier von innen nach außen gewechselt, und das war "unauffällig möglich", weil es neben dem Helm unterschlagen wurde. Mit Füllung der Zone neben dem Helm sieht man sofort, daß die gleiche goldene Innenseite b nicht an zwei Orten sein kann und wenige Millimeter daneben von der Innenseite zur Außenseite mutieren kann. Gehen wir zu Schnitt 3 und 4: Hier wird besagte nach vorne eingeschlagene goldene Innen-/Außenseite b vollends gewandelt und bildet ihrerseits die eingeschlagene goldene Außenseite b einer weiteren roten Zone a', die, wie in Schnitt 4 deutlich zu sehen, nicht mehr identisch mit a sein kann, weil deren oberer Abschluß die umgeklappte goldene Zone b bildet, und weil es zwei nichtidentische Unterkanten der beiden roten Zonen gibt, die eine nach unten gezaddelt, die andere unten stetig und rechts oben gezaddelt. Die frühere, ursprüngliche Außenseite a mutiert also erst zur Innenseite, um sich dann in zwei nicht identische Innenseiten a und a' aufzuteilen und sich so zwei neue Identitäten zuzulegen. Das seitlich eingeschlagene Gold wäre eigentlich Ebene b, aber da b jetzt ganz vorne und oben liegt, muß auch diese jetzt zwei Ebenen darunter liegende Ebene mit b' bezeichnet werden. Wie schon beim letzten Beispiel wird auch hier deutlich, daß jedes Auftreten einer gespaltenen Identität (a und a', b und b') nichts anderes als ein schwerer zeichnerischer Fehler ist. Was tun wir dagegen? Hier hilft nur die radikale Verschmelzung der Ebene a mit b, damit a' zum neuen b werden kann, jetzt bis zum Nacken verlängert. Das Ergebnis ist ein simpler Aufbau aus zwei Schichten, jederzeit nachvollziehbar, wie die vier Schnitte der unteren Reihe belegen. Auch hier sieht man, wie lohnend das Denken in Schnitten, Tiefenprofilen und Ebenen ist, denn so detektiert und löst man Fehler.

Bitte nehmen Sie als Botschaft mit: Es hilft sowohl beim Analysieren als auch beim Entwerfen, sich an allen komplexen Stellen das echte, gegebene oder gewünschte Tiefenprofil zu skizzieren. Und ehe man als Künstler seine Zeichnung dem zahlenden Kunden abliefert, hilft diese Plausibilitätsprüfung, einwandfreie Arbeit abzuliefern. Umgekehrt kann ich jedem Kunden nur raten, auf genau solche Stellen zu achten und ggf. auszudiskutieren.

Umgezeichnete reale Fälle mit Benennung der Problemstellen
Die nachfolgenden Graphiken basieren alle auf Wappenrolleneintragungen der letzten Jahre. Um niemanden bloßzustellen, wurden alle Vorlagen der wiedererkennbaren Motive beraubt sowie anonymisierend standardisiert neu und in einheitlichen Tinkturen skizziert, so daß Dritte weder den Künstler noch den Wappenträger identifizieren können. Dennoch beruhen alle Graphiken, auch die unterirdischsten, auf echten Fällen. Diese Zusammenstellung zeigt, wie nötig es ist, über dieses Thema zu reden, mit den Künstlern, mit den Wappenrollen, mit deren Kontrollgremien. Diese Zusammenstellung soll auf niemanden mit dem Finger zeigen, sondern helfen, es zukünftig gemeinsam besser zu machen und die Qualität zukünftiger Wappenrolleneintragungen zu heben. Und falls sich ein Künstler wiedererkennt: Sie können es besser, und ab heute machen Sie es auch besser, weil Sie gelernt haben, was falsch war und wie es besser geht!

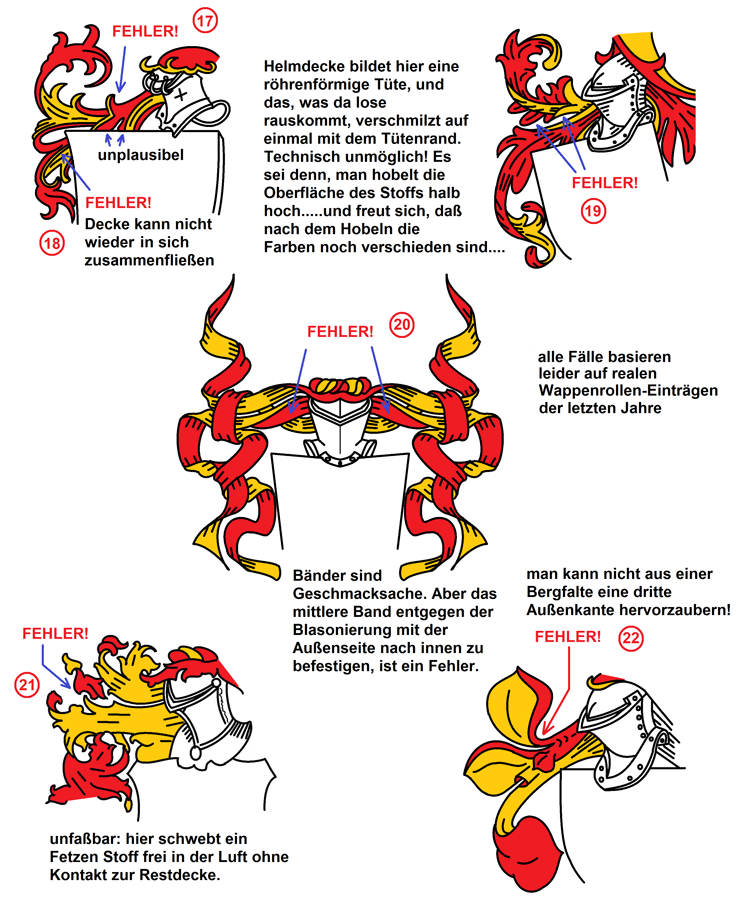
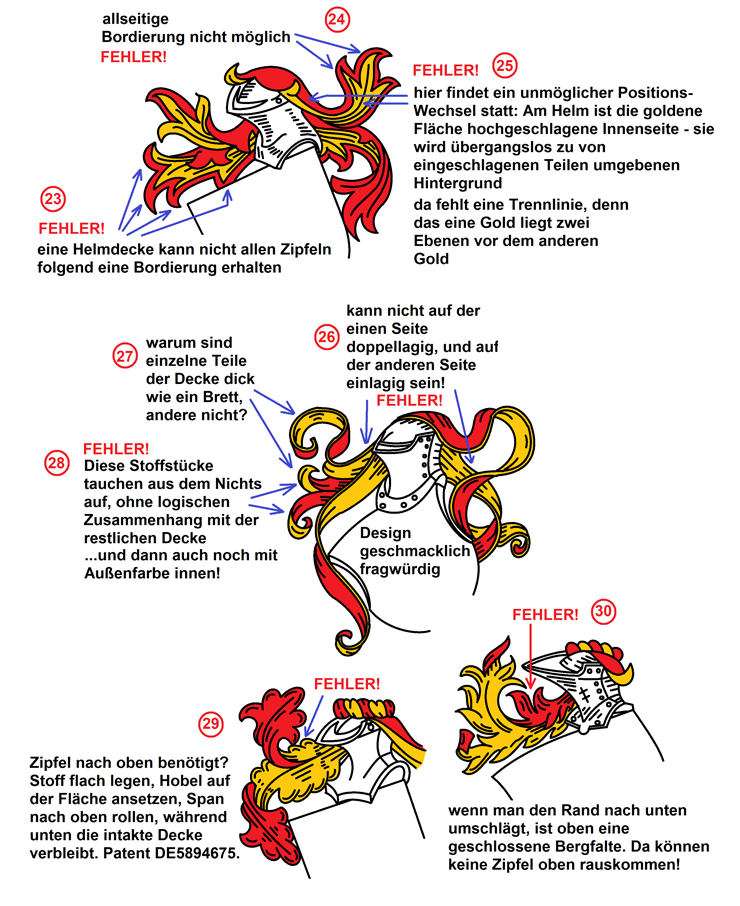
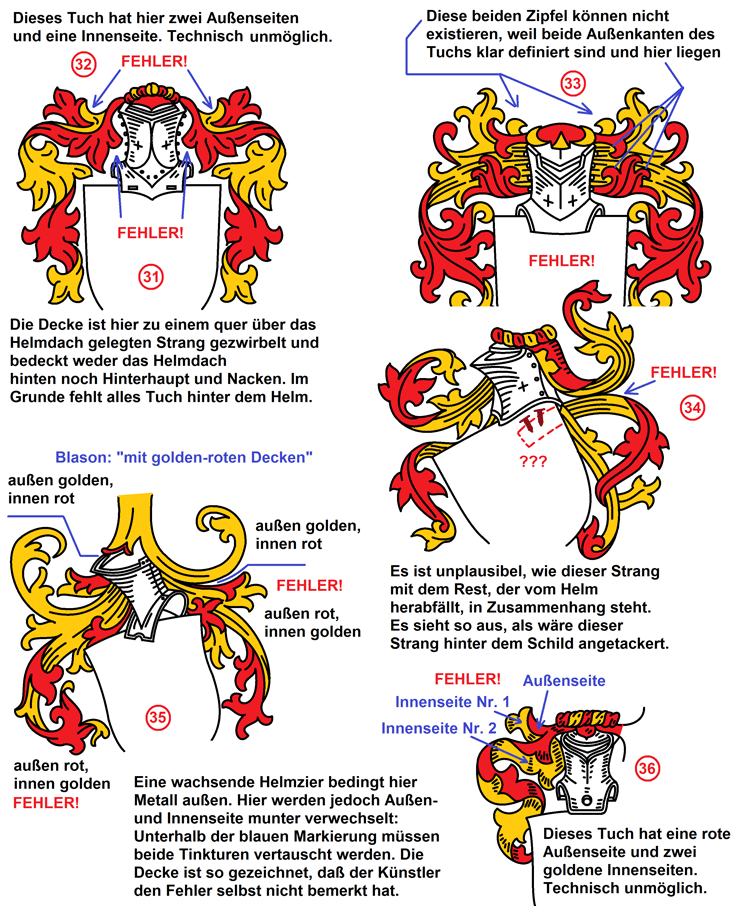
Fazit: Wer Fehler kennt, erkennt und vermeidet sie!
Es ist gewiß nicht einfach, Helmdecken zu zeichnen. Zum Glück ist Stoff seinem Wesen nach elastisch, biegsam, faltbar und dehnbar. Dies eröffnet uns wunderbare Gestaltungsmöglichkeiten. Wir dürfen jedoch niemals aus den Augen verlieren, daß der Tuchcharakter nicht verloren gehen darf. Ob in Lappen oder Bänder zerschnitten, ob ganz oder gezaddelt, ob drei oder 20 Windungen im Raum - ein Tuch ist ein Tuch und bleibt ein Tuch. Ein zusammenhängendes Tuch ohne lose Teile, denen die Anbindung an das Haupttuch fehlt. Ebenso trivial erscheint das Postulat, daß eine Helmdecke so gezeichnet werden muß, daß man die Decke nachvollziehen kann, daß man jeder Windung ansehen kann, ob sie richtig oder falsch ist. Ein zittriges Gekröse (versehentlich in der Kochwäsche gelandet?), das die Identifizierung von Innen- und Außenseite verunmöglicht und die Identität der einzelnen Stoffzüge auflöst, ist verfehlt. Und die Arbeit auf dem Papier oder am PC darf uns nicht verleiten, etwas zu machen, dem keine echte Situation entsprechen kann. Wie auch immer dargestellt, die Helmdecke muß technisch möglich sein. Sie sollte darüber hinaus für den Betrachter leicht nachvollziehbar sein, um insgesamt plausibel und authentisch zu wirken.

An dieser Stelle möchte ich nachhaltig von der unreflektierten Verwendung von fertigen Clips aus käuflichen Sammlungen o.ä. abraten. Deren Entwickler haben meistens sehr wenig Ahnung von Heraldik und pfeifen auf deren Regeln. Die Helmdecken aus solchen Clip-Sammlungen "machen was daher", halten aber keiner näheren Überprüfung stand. In der Regel sind Clip-Helmdecken (z. B. Armorial Gold) daher ohne zusätzliche Nachbearbeitung unbrauchbar. Lieber eine einfache, aber richtige Helmdecke selber zeichnen.

Helmdecken (1) - Helmdecken (2) - Fallstricke - Helmdecken am PC

Übersicht

Home